3.三分損益法
これまでの文献上からの推定として、それは前漢王朝の中期ごろとされていました。そ の都長安の行政機関の一つ、教坊(京坊又は京房とも)には宮廷音楽や歌舞の教習の寮 として、また雅楽や宴楽総ての司所として、これら一切を管掌する機構が措かれていたと言われています。
前章の記述のように王朝交代の度毎に、音律の基準を変え続けてきたために、それま での奏楽響態は、各楽器毎にその基本音律が異なり製作年代の離れた楽器ほど、その音 律や旋律が曖昧な響態となり、これに伴う器楽曲の曲調的濁りを解消し、透明な奏楽を 指向して、全音律のピッチを制定することにしたのです。
そして新たに製作した律管の音律を普遍的12本の竹管の12律として、楽器製作段 階の音律調整のゲージとしたのです。
その基本的音律を顕出するための作法が三分損益法だったわけです。この手法とは、響 態を持った弦を三等分したり、四等分したりしながら、秩序だって音律を顕出してゆく 作法のことです。
即ち三分とは、1本の弦を正確に三等分すること。損益とは損一法(捨一法とも)と 益一法(得一法とも)との、両者を併合した総称です。只単純に考えただけでも、一定 のテンションを損なうことなく、弦上の三等分の位置に印をつけることは、当時の作図 法を以ってしてもという疑問もさることながら、演繹法で算定すればそれはいとも簡単 といえます。
弦と同一の長さの薄紙の帯に、二つ折りを2回続ければ四等分点が得られます。
〔図の(1)参照〕
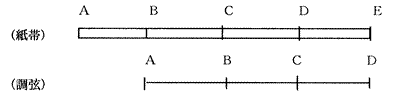
実際には,紙帯(図の1)のB点からEまでの弦を張り、紙帯のB点C点の寸尺で弦 に移して、弦上のA点B点に置き換えて、そこから作法を始めたようですが、ここでは 作法の理解を安易にするために、紙帯の長さと同一の弦を想定したまま、考察を進める ことにします。
まず三分損一とは、1本の弦の全長の三分一だけ短くした、即ち三分二の長さの位置 で発音された音律は、元の全長開放弦とは最も関係の深い協和音程がえられます。
ここで因みにメルセンスの法則を借りれば、〈弦の振動数は、その長さに反比例する〉 であることから、開放弦の振動数が2の倍数値とするなら、損一位置の振動数は、3の 倍数値となり、振動数は2:3の比率となるわけです。〔図の(2)参照〕
[図の2]
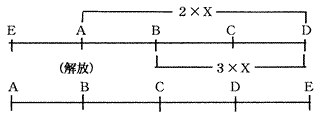
実はこの2音間(AD:BD)の音程は、純正調(以下この付記は略す)の音程では 完全5度と言う完全協和音の成立を意味します。
これを現代音楽の譜表に示せば[(譜例7)参照]、開放弦の音を c’(do)の調律として、損一の音は g’(sol)となります(譜例7図「イ」を参照)。従って完全5度 音程の2音間の振動数は2:3の倍数値の関係にあるわけです。つまり1対2(オクター ブ音程)とか2対3とか奇数対偶数の対比がシンプルなほど、より協和音関係が完全な ものとなるわけです。この1対2の2次的奇偶の対比は4:5そして5:4となります。 この音程関係は長3度と短6度となり、この複合的協和音関係は、3度6度と言う洋楽 2声並行音の定則性となり、不完全協和音と呼ばれているものであることを参考までに触れておきます。
さて次ぎの益一とは、前記の損一によって短くなったおなじ長さだけ逆方向に延ばし てこれに加えると、元の起音×全長音から完全4度下の音が得られます〔(図の(3)参 照〕。
[図の3]
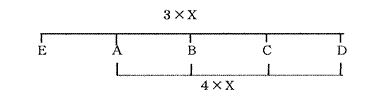
勿論古代中国では完全4度、5度と言った現代音楽的音程認識ではなく、自然的に心 地良い音律感だったわけでしょう。
こうして新たに顕出された図の3のC位置の音律は、先の損一の位置B位置の音とは 甲乙(オクターブ上下複合)の関係で、その振動数は1対2の倍数値となり、まさに完 全8度の完全協和音です。これを弦振動数値で表現を改めると、奇数・偶数値の最もシ ンプルな基本的数値対象となります。こうした損一と益一を1回ずつ継けた測定手法の 視尺が、即ち四等分法と謂われる所以でもあるわけです。
そしてこれを譜表上に示せば、次ぎの譜例7の「イ」と「ロ」となってきます。
[譜例・7]

こうして弦上の視尺した手法を、譜表にしめしてはじめて、完全5度や完全4度とい う現代的協和音を確認することが出来たわけで、偶々そうだったことにより、改めて往 時の漢民族の音律意識の高潔性に、只々首肯するほかはありません。
以上これまでは、三分損益法に関する作法とその音律的価値観を考察してみたわけで す。実際の作法の現場では、全長弦(開放弦)の延長下の音や、甲の音域を越えること もなく、ひたすら原音(起音・基音)から、オクターブの甲に向かって進めた課程で、現 代音楽のクロマチック12階音に限りなく近い十二律が顕出されていったわけです。